Sziasztok!

Következő feladatom egy tananyag elkészítése volt, "okostáblára".
Először végiggondoltam, melyik tananyag-rész lenne a feladatnak megfelelő, aztán eszembe jutott, hogy akármilyen nehéz is lesz, a logaritmust fogom választani. Emlékszem, anno mi is háborogtunk, hogy minek tanulunk logaritmust, hiszen a való életben sosem látunk ilyesmit, és úgysem fogjuk használni. Pedig valójában a természetes számolási mód a logaritmikus. Nos, akkor fogjunk is bele!

Módszer: RJR modell (Ráhangolódás - Jelentésteremtés - Reflektálás)

Először is, amit a matematika oktatásában nagyon hiányolok, hogy megértsük, mi mit jelent. Így az első oldal a logaritmus szó magyarázata. Aztán a felhasználása, hiszen az, hogy sosem fogunk az életben logaritmust látni, nagyon pontatlan, lévén maga a látásunk is logaritmikusan működik. Azaz, például ha van két ugyanolyan fényerejű izzónk, akkor azt nem kétszer olyan fényesnek látjuk, mintha egy lenne. Ahhoz, hogy kétszer fényesebbnek lássuk, 10 izzó kell. Ahhoz, hogy háromszor olyan fényesnek, 100 izzó, és így tovább. Ezek a 10 hatványai. A hallással ugyanígy vagyunk.
Elméletileg az összes érzékszervünk logaritmikusan működik, de én csupán a látásról és a hallásról szóló tanulmányokat találtam. Viszont van még egy halom dolog, amire szintén ráilleszthető egy logaritmikus skála. Ezek némelyike képen jelenik meg, és tanári magyarázat szükséges hozzá.

Ekkor jön be a képbe egy beágyazott videó. (~ 7 perc, mert levágtam az elejét és a végét.) Sajnos angolul van, aminek a feliratát nem sikerült már beillesztenem, úgyhogy angolos osztálynak való, avagy szinkrontolmácsolni kell hozzá.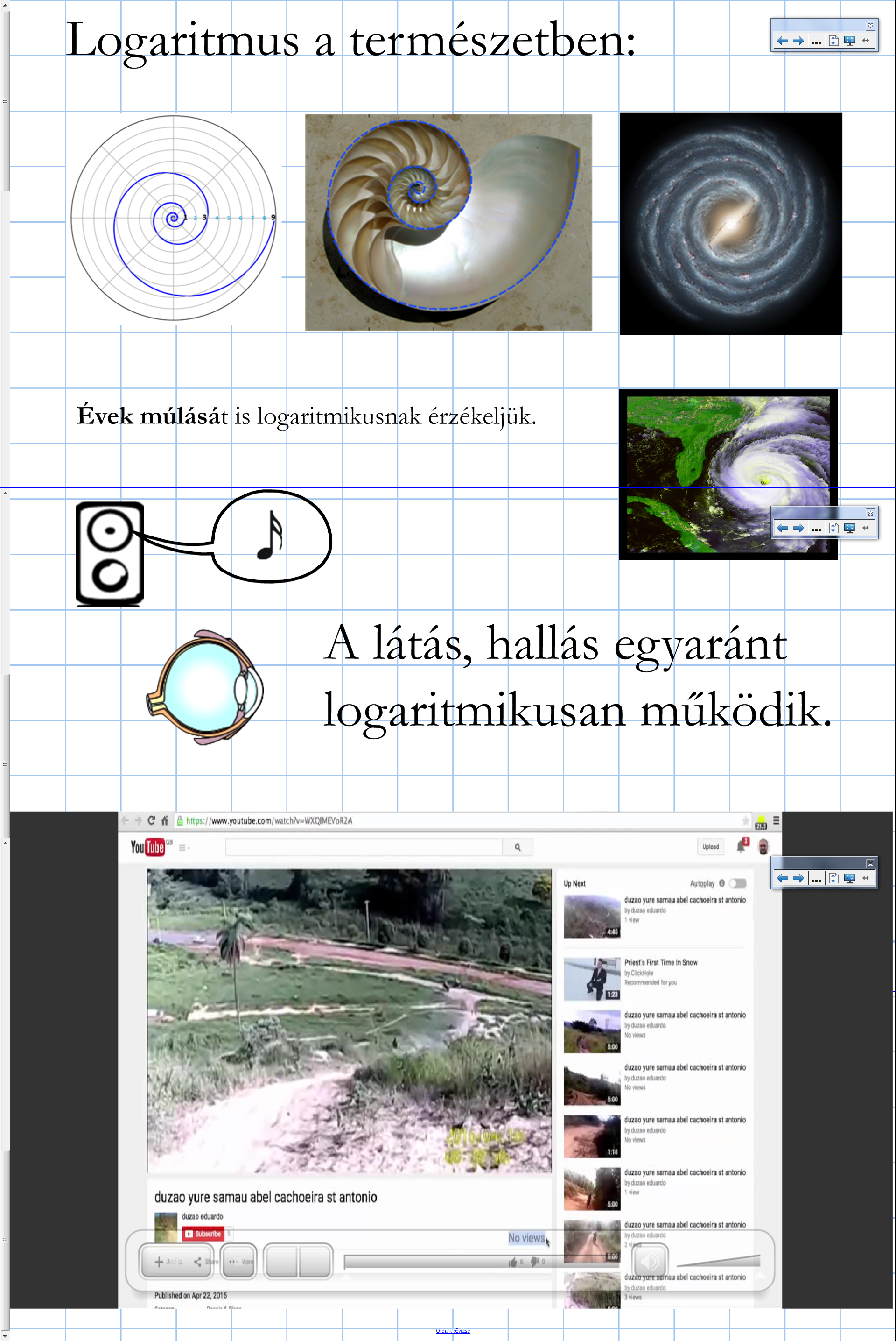

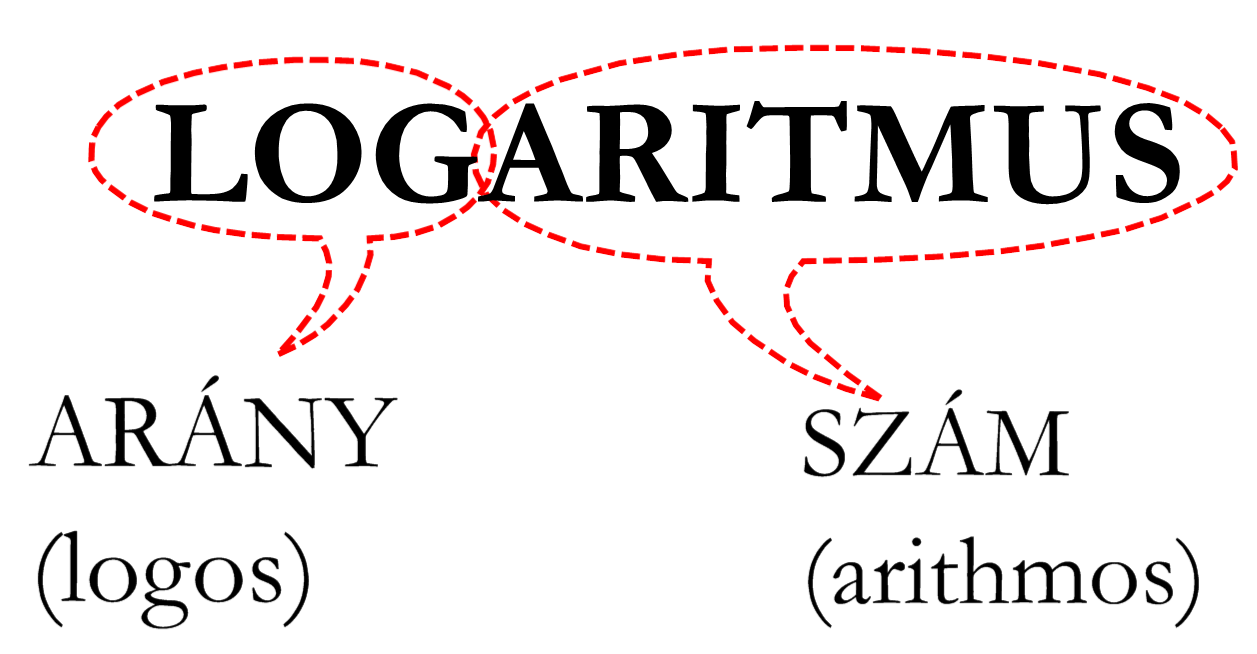
A videó után jöhet a logaritmikus skála megértése. Három különböző alapú skálát szerkesztettem, mindegyiknél meg lehet kérdezni, a "kék" számok milyen számok (hatványok). Észrevesszük, hogy ezek egyenlő távolságra vannak egymástól, míg a többi ezekhez képest arányosan. Íme a szó értelme: logos (arány) + arithmos (szám)!

Ekkor jöhet már a definíció és a jelölés, hiszen így már kicsit emészthetőbb a dolog. Az oldal alján egy (geogebrás) gyakorló oldal linkje van, ezen lehet a definíciót gyakorolni.

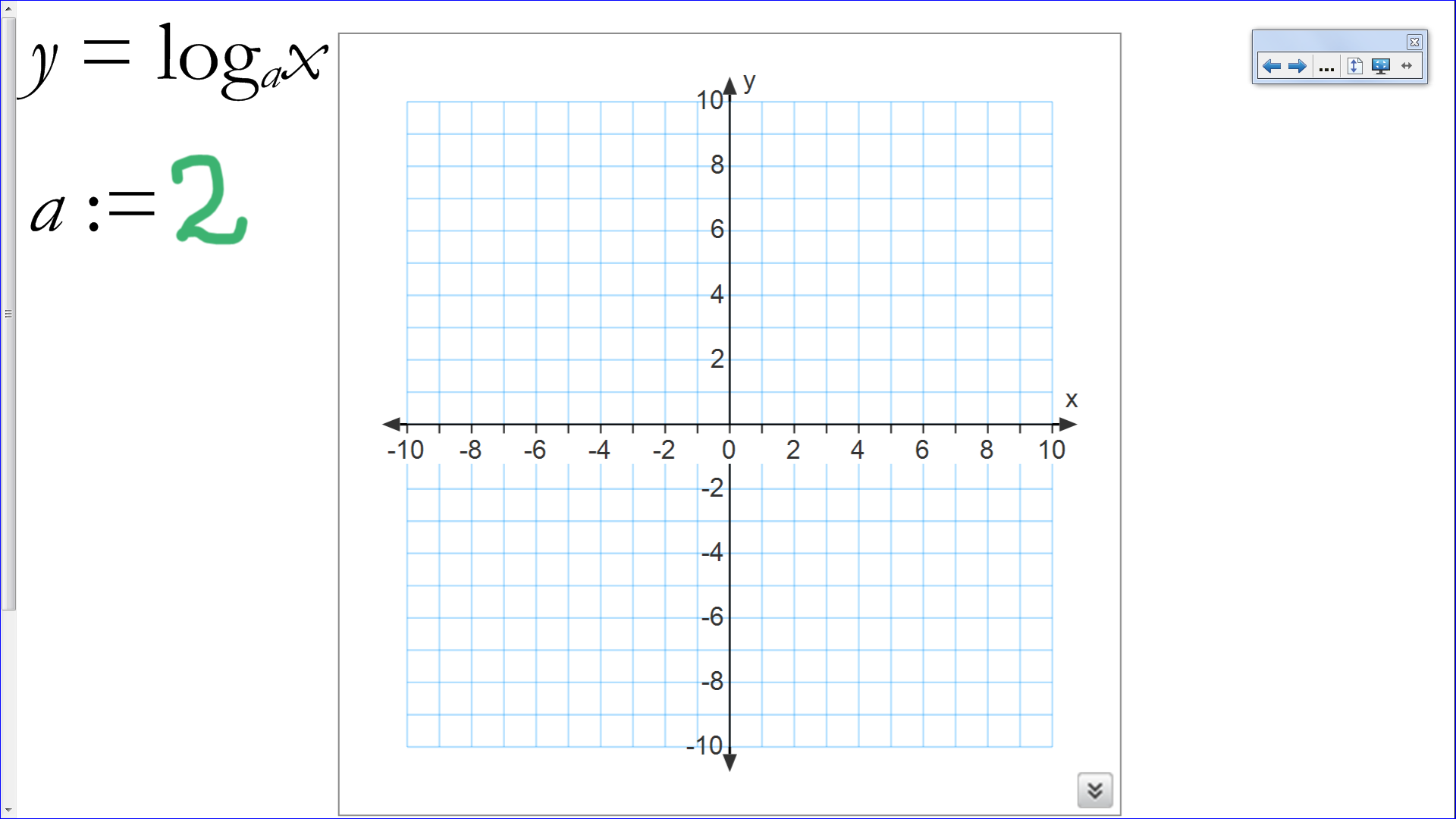
Aztán jöhet a logaritmusfüggvény: Kapásból feladat formájában. A táblán egy koordináta rendszer látható, bal felül a szabály, alatta pedig az alap, amelyet tetszés szerint változtathatunk. Először egy kettes alapú logaritmusfüggvény felrajzolása a feladat, itt akár egyesével kijöhetnek a diákok, és a grafikon pontjait (dupla kattintással) felrajzolhatják, majd összeköthetik. Addig a többiek a füzetbe rajzolnak. Ha ez kész, letörölhetjük, és jöhet a következő alap. Addig rajzolunk, amíg észre vesszük, hogy az egynél nagyobb alapú függvények szigorú monoton nőnek, a 0 és 1 közöttiek pedig csökkennek. Fontos tulajdonság!

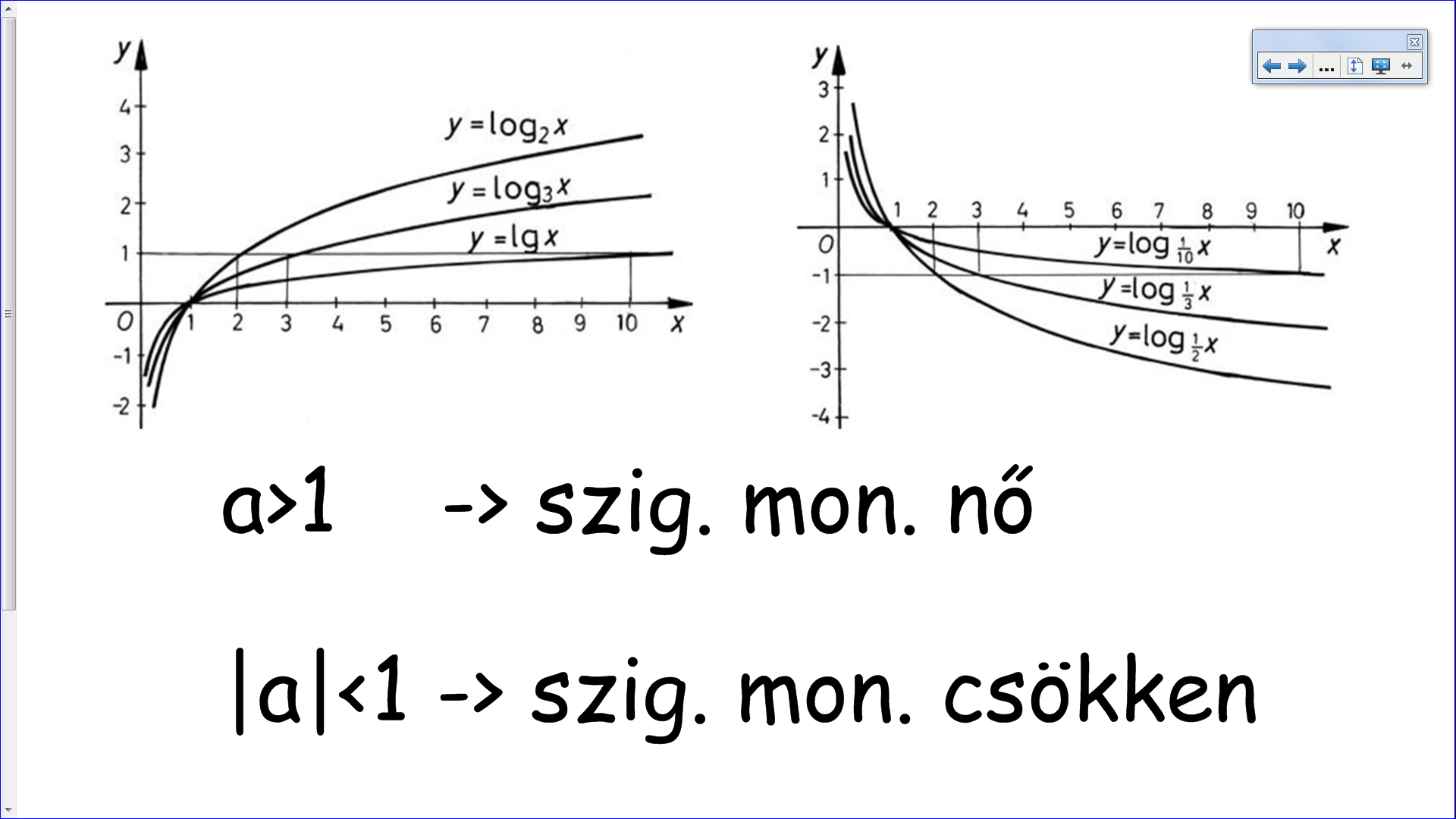
Mit kell még tudni? Azonosságokat! Ezeket egyesével bemutatjuk a gyerekeknek, akik szorgosan jegyzetelnek, avagy ki is adhatjuk az előre kinyomtatott verziót. Bár ez gyorsabb, fennáll a veszélye, hogy nem értik meg a mögöttes tartalmat, mert hiszen minek is figyeljenek oda azokra az unalmas bizonyításokra, ha itt van a kezemben a lényeg?

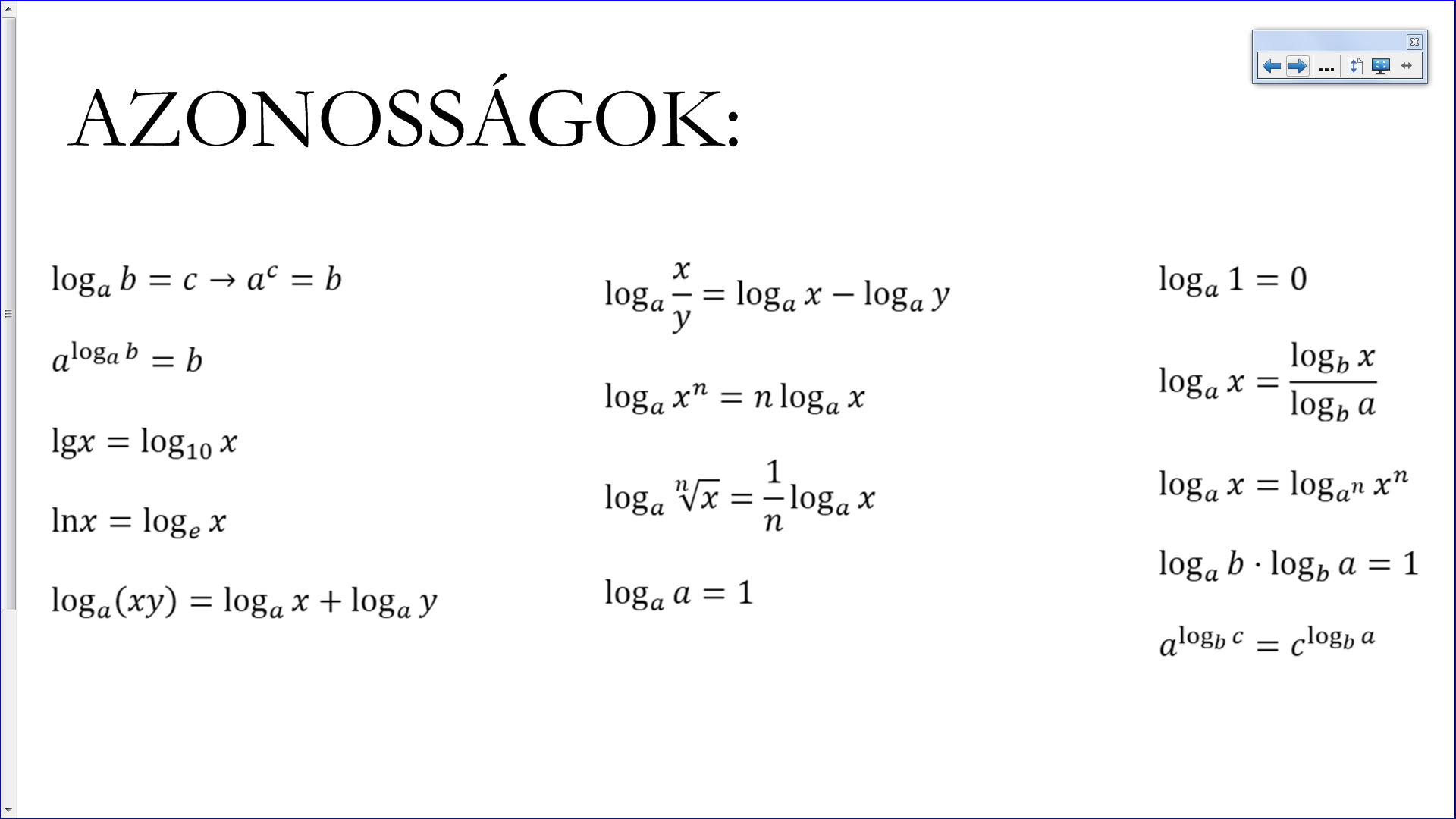
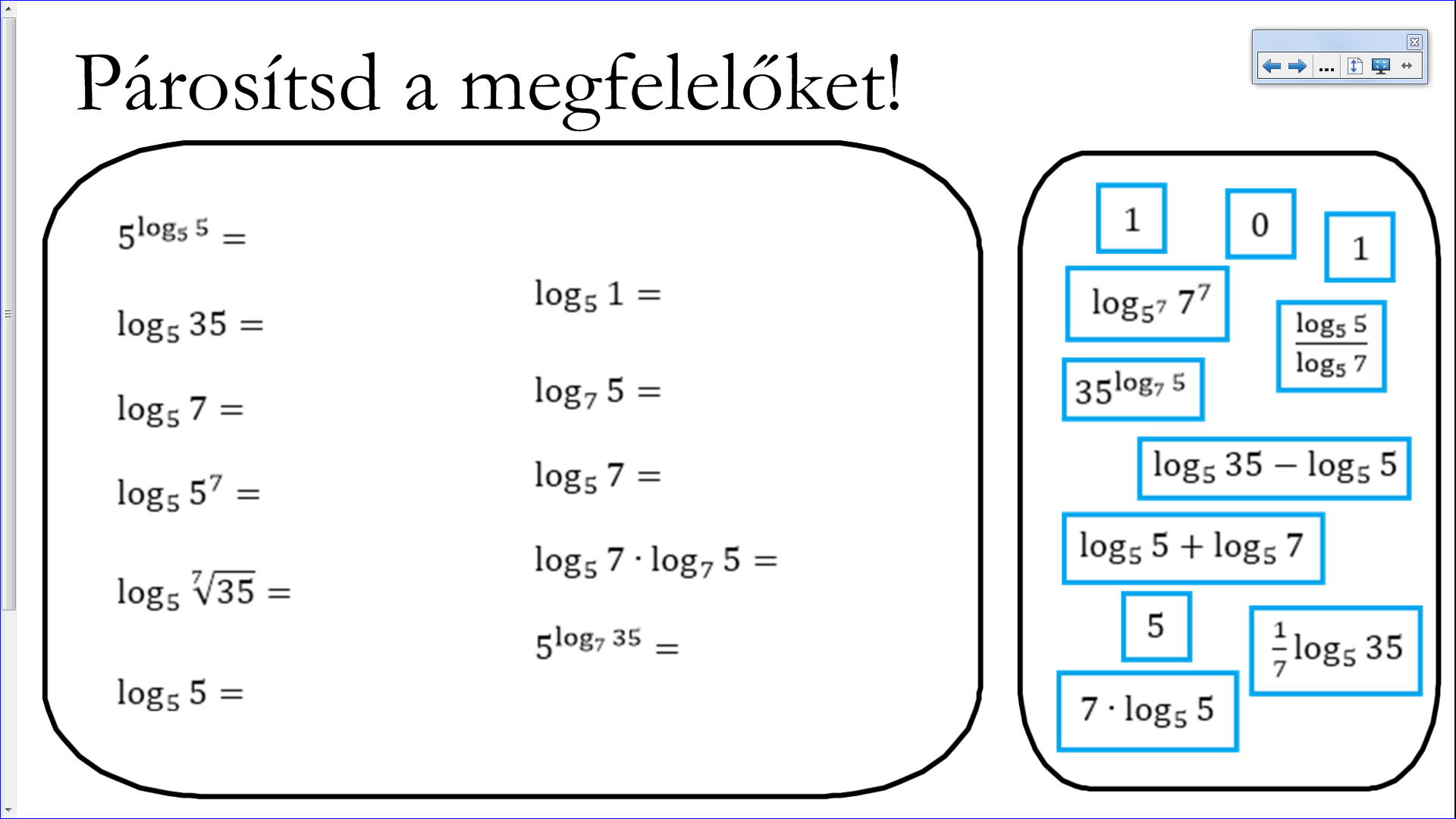
A gyakorlás elmaradhatatlan, így a következő oldalon található a párosító feladat, azaz találjuk meg az egyenlőség másik oldalát. Már konkrét behelyettesített számokkal dolgozunk, így még egyszer átnézetve a gyerekekkel az azonosságokat. Itt a feladat kinyomtatott verzióját ki lehet osztani, hogy aki nem a táblánál dolgozik, az is oldhassa a feladatot.

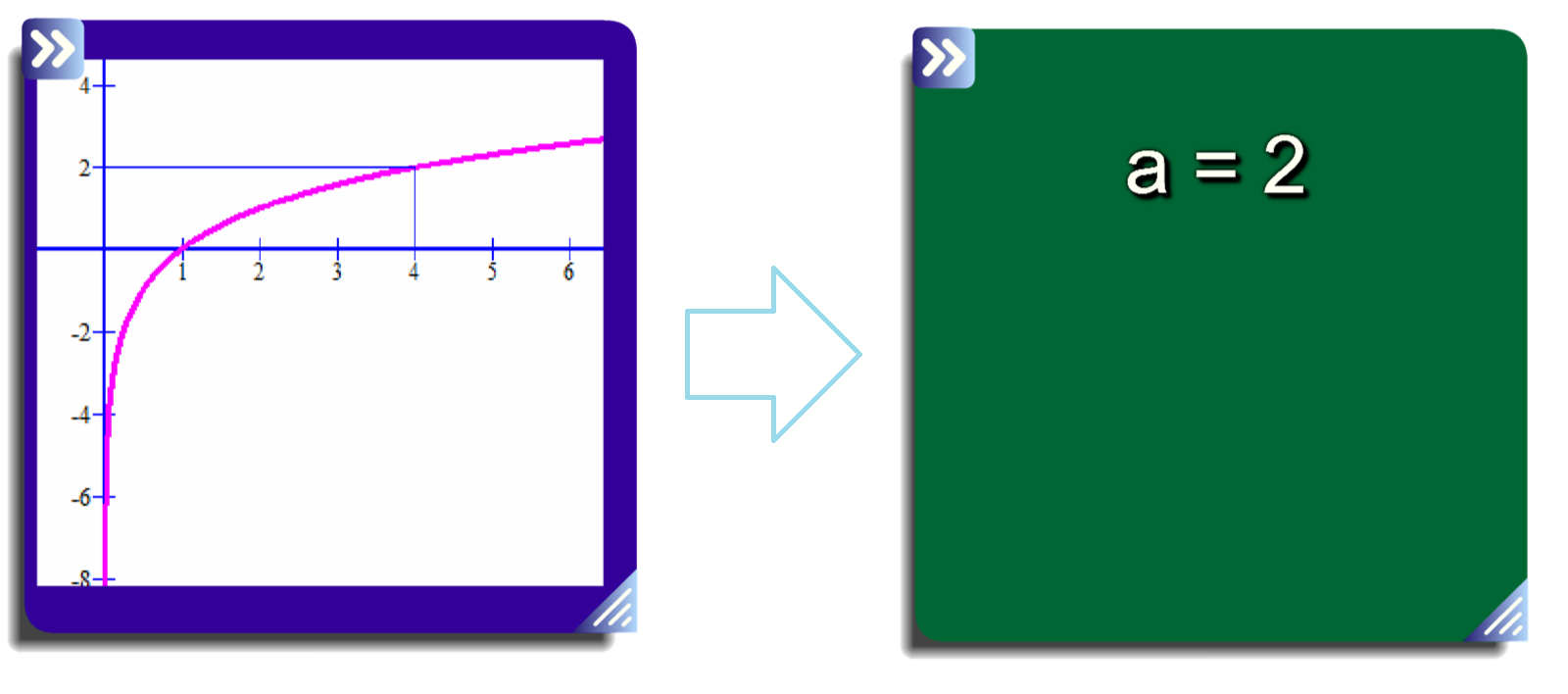
Végül egy utolsó feladat: A grafikon alapján mondd meg, milyen alapú logaritmusfüggvényt ábrázol! Akár szavazórendszerrel megoldható, akár az adott válaszokat a füzetbe jegyezzék fel. Amikor rákattintunk a grafikont tartalmazó kék "dobozra", az megfordul és fény derül a megoldásra. Négy ilyen típusú feladat van egymás alá helyezve, így akár egyesével is megoldathatjuk.

--x--x--x--x--x--x--x--x--x--x--x--x--x--x--x--x--x--x--x--x--x--x--x--x--x--x--x--x--x--x--x--x--x--x--x--x--x--x--x--x--

Eddig talán ez volt az a feladat, amely legjobban tetszett. A kezelendő felület érdekes, bár egyelőre még nincs meg a "digital fluency", így viszonylag hosszú időbe telt, amíg összeraktam. A programnak vannak olyan elemei, amelyeket máshogy írtam volna meg. Ilyen például az egyenletszerkesztő. A Word egyenletszerkesztője tökéletesen használható, itt viszont ici-pici ikonokkal van jelölve ráadásul nem is minden. Valamilyen általam megválasztott alapú logaritmust nem is sikerült beírnom, így azt egyszerűen alsóindex-szel, vagy a képlet (Wordben megírt) képével oldottam meg. Ettől eltekintve izgalmas volt kipróbálni egy ilyen felületet, és minden bizonnyal (ha lesz rá lehetőség) használni fogom.

Logaritmus.notebook fájl itt található.

Köszönöm az eheti figyelmet! További szép estét!